IMO Shortlist 2006 problem C7
Kvaliteta:
Avg: 0,0Težina:
Avg: 9,0 Consider a convex polyhaedron without parallel edges and without an edge parallel to any face other than the two faces adjacent to it. Call a pair of points of the polyhaedron antipodal if there exist two parallel planes passing through these points and such that the polyhaedron is contained between these planes. Let  be the number of antipodal pairs of vertices, and let
be the number of antipodal pairs of vertices, and let  be the number of antipodal pairs of midpoint edges. Determine the difference
be the number of antipodal pairs of midpoint edges. Determine the difference 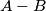 in terms of the numbers of vertices, edges, and faces.
in terms of the numbers of vertices, edges, and faces.
 be the number of antipodal pairs of vertices, and let
be the number of antipodal pairs of vertices, and let  be the number of antipodal pairs of midpoint edges. Determine the difference
be the number of antipodal pairs of midpoint edges. Determine the difference 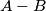 in terms of the numbers of vertices, edges, and faces.
in terms of the numbers of vertices, edges, and faces. Izvor: Međunarodna matematička olimpijada, shortlist 2006
 Školjka
Školjka 
