IMO Shortlist 2006 problem G6
Dodao/la:
arhiva2. travnja 2012. Circles
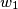
and
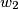
with centres
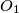
and
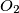
are externally tangent at point
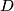
and internally tangent to a circle
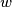
at points
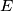
and
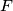
respectively. Line
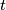
is the common tangent of
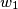
and
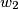
at
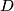
. Let

be the diameter of
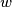
perpendicular to
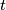
, so that
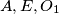
are on the same side of
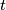
. Prove that lines
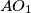
,
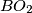
,
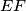
and
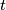
are concurrent.
%V0
Circles $w_{1}$ and $w_{2}$ with centres $O_{1}$ and $O_{2}$ are externally tangent at point $D$ and internally tangent to a circle $w$ at points $E$ and $F$ respectively. Line $t$ is the common tangent of $w_{1}$ and $w_{2}$ at $D$. Let $AB$ be the diameter of $w$ perpendicular to $t$, so that $A, E, O_{1}$ are on the same side of $t$. Prove that lines $AO_{1}$, $BO_{2}$, $EF$ and $t$ are concurrent.
Izvor: Međunarodna matematička olimpijada, shortlist 2006