IMO Shortlist 2008 problem C1
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 In the plane we consider rectangles whose sides are parallel to the coordinate axes and have positive length. Such a rectangle will be called a box. Two boxes intersect if they have a common point in their interior or on their boundary. Find the largest  for which there exist
for which there exist  boxes
boxes 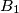 ,
,  ,
, 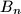 such that
such that 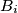 and
and  intersect if and only if
intersect if and only if 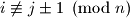 .
.
Proposed by Gerhard Woeginger, Netherlands
 for which there exist
for which there exist  boxes
boxes 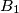 ,
,  ,
, 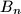 such that
such that 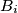 and
and  intersect if and only if
intersect if and only if 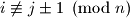 .
. Proposed by Gerhard Woeginger, Netherlands
Izvor: Međunarodna matematička olimpijada, shortlist 2008
 Školjka
Školjka