IMO Shortlist 2008 problem G4
Dodao/la:
arhiva2. travnja 2012. In an acute triangle
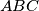
segments
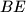
and
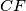
are altitudes. Two circles passing through the point

anf
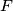
and tangent to the line
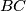
at the points

and
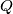
so that
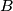
lies between

and
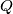
. Prove that lines
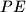
and
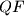
intersect on the circumcircle of triangle
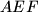
.
Proposed by Davood Vakili, Iran
%V0
In an acute triangle $ABC$ segments $BE$ and $CF$ are altitudes. Two circles passing through the point $A$ anf $F$ and tangent to the line $BC$ at the points $P$ and $Q$ so that $B$ lies between $C$ and $Q$. Prove that lines $PE$ and $QF$ intersect on the circumcircle of triangle $AEF$.
Proposed by Davood Vakili, Iran
Izvor: Međunarodna matematička olimpijada, shortlist 2008