IMO Shortlist 2009 problem C6
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 On a 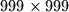 board a limp rook can move in the following way: From any square it can move to any of its adjacent squares, i.e. a square having a common side with it, and every move must be a turn, i.e. the directions of any two consecutive moves must be perpendicular. A non-intersecting route of the limp rook consists of a sequence of pairwise different squares that the limp rook can visit in that order by an admissible sequence of moves. Such a non-intersecting route is called cyclic, if the limp rook can, after reaching the last square of the route, move directly to the first square of the route and start over.
board a limp rook can move in the following way: From any square it can move to any of its adjacent squares, i.e. a square having a common side with it, and every move must be a turn, i.e. the directions of any two consecutive moves must be perpendicular. A non-intersecting route of the limp rook consists of a sequence of pairwise different squares that the limp rook can visit in that order by an admissible sequence of moves. Such a non-intersecting route is called cyclic, if the limp rook can, after reaching the last square of the route, move directly to the first square of the route and start over.
How many squares does the longest possible cyclic, non-intersecting route of a limp rook visit?
Proposed by Nikolay Beluhov, Bulgaria
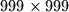 board a limp rook can move in the following way: From any square it can move to any of its adjacent squares, i.e. a square having a common side with it, and every move must be a turn, i.e. the directions of any two consecutive moves must be perpendicular. A non-intersecting route of the limp rook consists of a sequence of pairwise different squares that the limp rook can visit in that order by an admissible sequence of moves. Such a non-intersecting route is called cyclic, if the limp rook can, after reaching the last square of the route, move directly to the first square of the route and start over.
board a limp rook can move in the following way: From any square it can move to any of its adjacent squares, i.e. a square having a common side with it, and every move must be a turn, i.e. the directions of any two consecutive moves must be perpendicular. A non-intersecting route of the limp rook consists of a sequence of pairwise different squares that the limp rook can visit in that order by an admissible sequence of moves. Such a non-intersecting route is called cyclic, if the limp rook can, after reaching the last square of the route, move directly to the first square of the route and start over. How many squares does the longest possible cyclic, non-intersecting route of a limp rook visit?
Proposed by Nikolay Beluhov, Bulgaria
Izvor: Međunarodna matematička olimpijada, shortlist 2009
 Školjka
Školjka 
