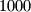
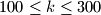
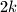
Suppose that students are standing in a circle. Prove that there exists an integer with such that in this circle there exists a contiguous group of students, for which the first half contains the same number of girls as the second half.
Proposed by Gerhard Wöginger, Austria
%V0
Suppose that $1000$ students are standing in a circle. Prove that there exists an integer $k$ with $100 \leq k \leq 300$ such that in this circle there exists a contiguous group of $2k$ students, for which the first half contains the same number of girls as the second half.
Proposed by Gerhard Wöginger, Austria
Izvor: Međunarodna matematička olimpijada, shortlist 2011
Školjka 
students are standing in a circle. Prove that there exists an integer 
with 
such that in this circle there exists a contiguous group of 
students, for which the first half contains the same number of girls as the second half.