IMO Shortlist 2012 problem A6
Dodao/la:
arhiva3. studenoga 2013. Let
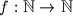
be a function, and let
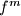
be
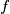
applied

times. Suppose that for every
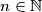
there exists a
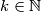
such that
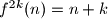
, and let
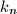
be the smallest such

. Prove that the sequence
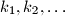
is unbounded.
%V0
Let $f: \mathbb{N} \rightarrow \mathbb{N}$ be a function, and let $f^m$ be $f$ applied $m$ times. Suppose that for every $n \in \mathbb{N}$ there exists a $k \in \mathbb{N}$ such that $f^{2k}(n)=n+k$, and let $k_n$ be the smallest such $k$. Prove that the sequence $k_1,k_2,\ldots$ is unbounded.
Izvor: Međunarodna matematička olimpijada, shortlist 2012