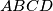
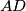
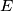
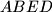
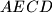
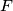
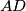
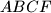
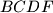
Let be a convex quadrilateral with non-parallel sides and . Assume that there is a point on the side such that the quadrilaterals and are circumscribed. Prove that there is a point on the side such that the quadrilaterals and are circumscribed if and only if is parallel to .
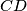
%V0
Let $ABCD$ be a convex quadrilateral with non-parallel sides $BC$ and $AD$. Assume that there is a point $E$ on the side $BC$ such that the quadrilaterals $ABED$ and $AECD$ are circumscribed. Prove that there is a point $F$ on the side $AD$ such that the quadrilaterals $ABCF$ and $BCDF$ are circumscribed if and only if $AB$ is parallel to $CD$.
Izvor: Međunarodna matematička olimpijada, shortlist 2012
Školjka 
be a convex quadrilateral with non-parallel sides 
and 
. Assume that there is a point 
on the side 
and 
are circumscribed. Prove that there is a point 
on the side 
and 
are circumscribed if and only if 
is parallel to 
.