Školjka

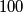We are given an infinite deck of cards, each with a real number on it. For every real number $x$, there is exacly one card in the deck that has $x$ written on it. Now two players draw disjoint sets $A$ and $B$ of $100$ cards each from this deck. We would like to define a rule that declares one of them a winner. This rule should satisfy the following conditions: \begin{enumerate} \item The winner only depends on the relative order of the $200$ cards: if the cards are leid down in increasing order face down and we are told which card belongs to which player, but not what numbers are written on them, we can still decide the winner. \item If we write the elements of both sets in increasing order as $A = \{a_1, a_2, \ldots, a_{100}\}$ and $B = \{b_1, b_2, \ldots, b_{100}\}$, and $a_i > b_i$ for all $i$, the $A$ beats $B$. \item If three players draw three disjoint sets $A, B, C$ from the deck, $A$ betas $B$ and $B$ beats $C$, then $A$ also beats $C$. \end{enumerate} How many ways are there define such a rule? Here, we consider the rules as different if there exist two sets $A$ and $B$ such that $A$ beats $B$ according to the rule, but $B$ beats $A$ according to the other. \begin{flushright}\emph{(Russia)}\end{flushright}