IMO Shortlist 2015 problem C2
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0We say that a finite set 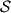 of points in the plane is balanced if, for any two different points
of points in the plane is balanced if, for any two different points  and
and  in
in 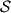 , there is a point
, there is a point 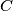 in
in 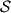 such that
such that 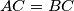 . We say that
. We say that 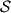 is centre-free if for any three different points
is centre-free if for any three different points  ,
,  and
and 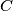 in
in 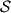 , there is no points
, there is no points  in
in 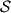 such that
such that 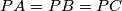 .
.
(a) Show that for all integers 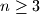 , there exists a balanced set consisting of
, there exists a balanced set consisting of  points.
points.
(b) Determine all integers 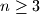 for which there exists a balanced centre-free set consisting of
for which there exists a balanced centre-free set consisting of  points.
points.
(Netherlands)
Izvor: https://www.imo-official.org/problems/IMO2015SL.pdf
 Školjka
Školjka 
