IMO Shortlist 2015 problem C4
Kvaliteta:
Avg: 3,0Težina:
Avg: 7,0Let  be a positive integer. Two players
be a positive integer. Two players  and
and  play a game in which they take turns choosing positive integers
play a game in which they take turns choosing positive integers 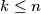 . The rules of the game are:
. The rules of the game are:
(i) A player cannot choose a number that has been chosen by either player on any previous turn.
(ii) A player cannot choose a number consecutive to any of those the player has already chosen on any previous turn.
(iii) The game is a draw if all numbers have been chosen; otherwise the player who cannot choose a number anymore loses the game.
The player  takes the first turn. Determine the outcome of the game, assuming that both players use optimal strategies.
takes the first turn. Determine the outcome of the game, assuming that both players use optimal strategies.
(Finland)
Izvor: https://www.imo-official.org/problems/IMO2015SL.pdf
 Školjka
Školjka 
