IMO Shortlist 2015 problem G5
Kvaliteta:
Avg: 2,7Težina:
Avg: 8,0Let 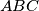 be a triangle with
be a triangle with 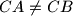 . Let
. Let  ,
, 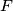 , and
, and 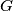 be the midpoints of the sides
be the midpoints of the sides  ,
, 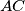 , and
, and 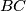 respectively. A circle
respectively. A circle 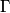 passing through
passing through  and tangent to
and tangent to  at
at 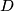 meets the segments
meets the segments 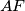 and
and 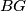 at
at 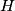 and
and 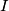 , respectively. The points
, respectively. The points 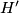 and
and 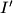 are symmetric to
are symmetric to 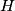 and
and 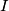 about
about 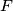 and
and 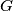 , respectively. The line
, respectively. The line 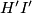 meets
meets 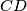 and
and 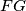 at
at 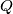 and
and 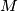 , respectively. The line
, respectively. The line 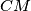 meets
meets 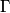 again at
again at  . Prove that
. Prove that 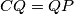 .
.
(El Salvador)
Izvor: https://www.imo-official.org/problems/IMO2015SL.pdf
 Školjka
Školjka