Školjka

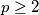Let $ p \geq 2$ be a prime number. Eduardo and Fernando play the following game making moves alternately: in each move, the current player chooses an index 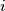$i$ in the set 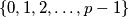$\{0,1,2,\ldots, p-1 \}$ that was not chosen before by either of the two players and then chooses an element 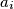$a_i$ from the set 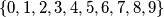$\{0,1,2,3,4,5,6,7,8,9\}$. Eduardo has the first move. The game ends after all the indices have been chosen .Then the following number is computed: 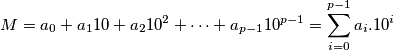$$M=a_0+a_110+a_210^2+\cdots+a_{p-1}10^{p-1}= \sum_{i=0}^{p-1}a_i.10^i$$. 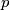The goal of Eduardo is to make $M$ divisible by $p$, and the goal of Fernando is to prevent this. Prove that Eduardo has a winning strategy.