Školjka IMO Shortlist 1960 problem 7
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0
An isosceles trapezoid with bases 
and 
and altitude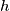 
is given.
a) On the axis of symmetry of this trapezoid, find all points
such that both legs of the trapezoid subtend right angles at ;
b) Calculate the distance of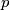
from either base;
c) Determine under what conditions such points actually exist. Discuss various cases that might arise.
and and altitude 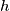is given. a) On the axis of symmetry of this trapezoid, find all points
such that both legs of the trapezoid subtend right angles at ; b) Calculate the distance of
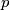from either base; c) Determine under what conditions such points
actually exist. Discuss various cases that might arise. Izvor: Međunarodna matematička olimpijada, shortlist 1960