IMO Shortlist 1961 problem 6
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Consider a plane  and three non-collinear points
and three non-collinear points 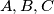 on the same side of
on the same side of  ; suppose the plane determined by these three points is not parallel to
; suppose the plane determined by these three points is not parallel to  . In plane
. In plane  take three arbitrary points
take three arbitrary points 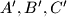 . Let
. Let 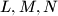 be the midpoints of segments
be the midpoints of segments 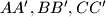 ; Let
; Let 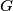 be the centroid of the triangle
be the centroid of the triangle 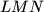 . (We will not consider positions of the points
. (We will not consider positions of the points 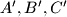 such that the points
such that the points 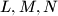 do not form a triangle.) What is the locus of point
do not form a triangle.) What is the locus of point 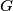 as
as 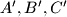 range independently over the plane
range independently over the plane  ?
?
 and three non-collinear points
and three non-collinear points 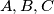 on the same side of
on the same side of  ; suppose the plane determined by these three points is not parallel to
; suppose the plane determined by these three points is not parallel to  . In plane
. In plane  take three arbitrary points
take three arbitrary points 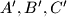 . Let
. Let 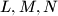 be the midpoints of segments
be the midpoints of segments 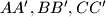 ; Let
; Let 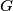 be the centroid of the triangle
be the centroid of the triangle 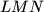 . (We will not consider positions of the points
. (We will not consider positions of the points 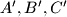 such that the points
such that the points 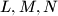 do not form a triangle.) What is the locus of point
do not form a triangle.) What is the locus of point 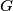 as
as 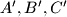 range independently over the plane
range independently over the plane  ?
? Izvor: Međunarodna matematička olimpijada, shortlist 1961
 Školjka
Školjka 
