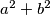
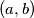
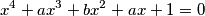
Determine the minimum value of when traverses all the pairs of real numbers for which the equation has at least one real root.
%V0
Determine the minimum value of $a^{2} + b^{2}$ when $(a,b)$ traverses all the pairs of real numbers for which the equation $$x^{4} + ax^{3} + bx^{2} + ax + 1 = 0$$ has at least one real root.
Izvor: Međunarodna matematička olimpijada, shortlist 1973
Školjka 
when 
traverses all the pairs of real numbers for which the equation 
has at least one real root.