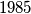
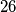
Given a set of positive integers, none of which has a prime divisor larger than , prove that the set has four distinct elements whose geometric mean is an integer.
%V0
Given a set $M$ of $1985$ positive integers, none of which has a prime divisor larger than $26$, prove that the set has four distinct elements whose geometric mean is an integer.
Izvor: Međunarodna matematička olimpijada, shortlist 1985
Školjka 
of 
positive integers, none of which has a prime divisor larger than 
, prove that the set has four distinct elements whose geometric mean is an integer.