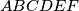
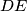
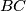
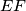
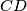
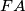
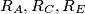
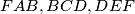
Let be a convex hexagon such that is parallel to , is parallel to , and is parallel to . Let denote the circumradii of triangles , respectively, and let denote the perimeter of the hexagon. Prove that
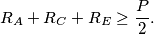
%V0
Let $ABCDEF$ be a convex hexagon such that $AB$ is parallel to $DE$, $BC$ is parallel to $EF$, and $CD$ is parallel to $FA$. Let $R_{A},R_{C},R_{E}$ denote the circumradii of triangles $FAB,BCD,DEF$, respectively, and let $P$ denote the perimeter of the hexagon. Prove that
$$R_{A} + R_{C} + R_{E}\geq \frac {P}{2}.$$
Izvor: Međunarodna matematička olimpijada, shortlist 1996
Školjka 
be a convex hexagon such that 
is parallel to 
, 
is parallel to 
, and 
is parallel to 
. Let 
denote the circumradii of triangles 
, respectively, and let 
denote the perimeter of the hexagon. Prove that 