IMO Shortlist 2006 problem C2
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 Let  be a regular
be a regular 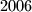 -gon. A diagonal is called good if its endpoints divide the boundary of
-gon. A diagonal is called good if its endpoints divide the boundary of  into two parts, each composed of an odd number of sides of
into two parts, each composed of an odd number of sides of  . The sides of
. The sides of  are also called good.
are also called good.
Suppose has been dissected into triangles by
has been dissected into triangles by 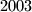 diagonals, no two of which have a common point in the interior of
diagonals, no two of which have a common point in the interior of  . Find the maximum number of isosceles triangles having two good sides that could appear in such a configuration.
. Find the maximum number of isosceles triangles having two good sides that could appear in such a configuration.
 be a regular
be a regular 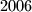 -gon. A diagonal is called good if its endpoints divide the boundary of
-gon. A diagonal is called good if its endpoints divide the boundary of  into two parts, each composed of an odd number of sides of
into two parts, each composed of an odd number of sides of  . The sides of
. The sides of  are also called good.
are also called good. Suppose
 has been dissected into triangles by
has been dissected into triangles by 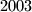 diagonals, no two of which have a common point in the interior of
diagonals, no two of which have a common point in the interior of  . Find the maximum number of isosceles triangles having two good sides that could appear in such a configuration.
. Find the maximum number of isosceles triangles having two good sides that could appear in such a configuration. Izvor: Međunarodna matematička olimpijada, shortlist 2006
 Školjka
Školjka 
