IMO Shortlist 2011 problem A6
Dodao/la:
arhiva23. lipnja 2013. Let
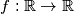
be a real-valued function defined on the set of real numbers that satisfies
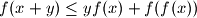
for all real numbers

and
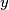
. Prove that
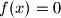
for all
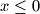
.
Proposed by Igor Voronovich, Belarus
%V0
Let $f : \mathbb R \to \mathbb R$ be a real-valued function defined on the set of real numbers that satisfies
$$f(x + y) \leq yf(x) + f(f(x))$$
for all real numbers $x$ and $y$. Prove that $f(x) = 0$ for all $x \leq 0$.
Proposed by Igor Voronovich, Belarus
Izvor: Međunarodna matematička olimpijada, shortlist 2011