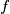
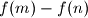
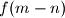
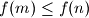
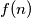
Let be a function from the set of integers to the set of positive integers. Suppose that, for any two integers and , the difference is divisible by . Prove that, for all integers and with , the number is divisible by .
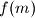
Proposed by Mahyar Sefidgaran, Iran
%V0
Let $f$ be a function from the set of integers to the set of positive integers. Suppose that, for any two integers $m$ and $n$, the difference $f(m) - f(n)$ is divisible by $f(m- n)$. Prove that, for all integers $m$ and $n$ with $f(m) \leq f(n)$, the number $f(n)$ is divisible by $f(m)$.
Proposed by Mahyar Sefidgaran, Iran
Izvor: Međunarodna matematička olimpijada, shortlist 2011
Školjka 
be a function from the set of integers to the set of positive integers. Suppose that, for any two integers 
and 
, the difference 
is divisible by 
. Prove that, for all integers 
, the number 
is divisible by 
.