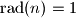
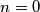
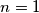
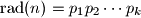
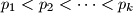
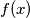
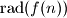
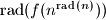
For a nonnegative integer define if or , and where are all prime factors of . Find all polynomials with nonnegative integer coefficients such that divides for every nonnegative integer .
%V0
For a nonnegative integer $n$ define $\text{rad}(n)=1$ if $n=0$ or $n=1$, and $\text{rad}(n)=p_1p_2\cdots p_k$ where $p_1<p_2<\cdots <p_k$ are all prime factors of $n$. Find all polynomials $f(x)$ with nonnegative integer coefficients such that $\text{rad}(f(n))$ divides $\text{rad}(f(n^{\text{rad}(n)}))$ for every nonnegative integer $n$.
Source: Međunarodna matematička olimpijada, shortlist 2012
Školjka 
define 
if 
or 
, and 
where 
are all prime factors of 
with nonnegative integer coefficients such that 
divides 
for every nonnegative integer