IMO Shortlist 1965 problem 2
Dodao/la:
arhiva2. travnja 2012. Consider the sytem of equations
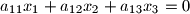
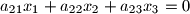
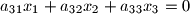
with unknowns
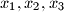
. The coefficients satisfy the conditions:
a)
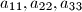
are positive numbers;
b) the remaining coefficients are negative numbers;
c) in each equation, the sum ofthe coefficients is positive.
Prove that the given system has only the solution
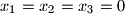
.
%V0
Consider the sytem of equations
$$a_{11}x_1+a_{12}x_2+a_{13}x_3 = 0$$ $$a_{21}x_1+a_{22}x_2+a_{23}x_3 =0$$ $$a_{31}x_1+a_{32}x_2+a_{33}x_3 = 0$$ with unknowns $x_1, x_2, x_3$. The coefficients satisfy the conditions:
a) $a_{11}, a_{22}, a_{33}$ are positive numbers;
b) the remaining coefficients are negative numbers;
c) in each equation, the sum ofthe coefficients is positive.
Prove that the given system has only the solution $x_1=x_2=x_3=0$.
Izvor: Međunarodna matematička olimpijada, shortlist 1965