IMO Shortlist 1977 problem 10
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let  be a given number greater than 2. We consider the set
be a given number greater than 2. We consider the set 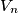 of all the integers of the form
of all the integers of the form 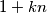 with
with 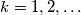 A number
A number  from
from 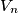 is called indecomposable in
is called indecomposable in 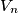 if there are not two numbers
if there are not two numbers 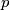 and
and 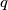 from
from 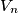 so that
so that 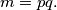 Prove that there exist a number
Prove that there exist a number 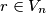 that can be expressed as the product of elements indecomposable in
that can be expressed as the product of elements indecomposable in 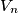 in more than one way. (Expressions which differ only in order of the elements of
in more than one way. (Expressions which differ only in order of the elements of 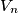 will be considered the same.)
will be considered the same.)
 be a given number greater than 2. We consider the set
be a given number greater than 2. We consider the set 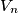 of all the integers of the form
of all the integers of the form 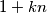 with
with 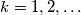 A number
A number  from
from 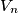 is called indecomposable in
is called indecomposable in 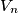 if there are not two numbers
if there are not two numbers 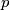 and
and 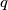 from
from 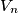 so that
so that 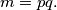 Prove that there exist a number
Prove that there exist a number 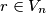 that can be expressed as the product of elements indecomposable in
that can be expressed as the product of elements indecomposable in 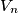 in more than one way. (Expressions which differ only in order of the elements of
in more than one way. (Expressions which differ only in order of the elements of 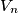 will be considered the same.)
will be considered the same.) Izvor: Međunarodna matematička olimpijada, shortlist 1977
 Školjka
Školjka 
