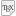IMO Shortlist 1978 problem 13
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 We consider a fixed point  in the interior of a fixed sphere
in the interior of a fixed sphere We construct three segments
We construct three segments 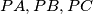 , perpendicular two by two
, perpendicular two by two with the vertexes
with the vertexes 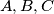 on the sphere
on the sphere We consider the vertex
We consider the vertex 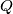 which is opposite to
which is opposite to  in the parallelepiped (with right angles) with
in the parallelepiped (with right angles) with 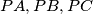 as edges
as edges Find the locus of the point
Find the locus of the point 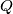 when
when 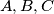 take all the positions compatible with our problem.
take all the positions compatible with our problem.
 in the interior of a fixed sphere
in the interior of a fixed sphere We construct three segments
We construct three segments 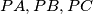 , perpendicular two by two
, perpendicular two by two with the vertexes
with the vertexes 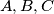 on the sphere
on the sphere We consider the vertex
We consider the vertex 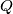 which is opposite to
which is opposite to  in the parallelepiped (with right angles) with
in the parallelepiped (with right angles) with 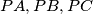 as edges
as edges Find the locus of the point
Find the locus of the point 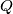 when
when 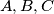 take all the positions compatible with our problem.
take all the positions compatible with our problem. Izvor: Međunarodna matematička olimpijada, shortlist 1978
 Školjka
Školjka