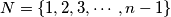
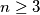
Each of the numbers in the set , where , is colored with one of two colors, say red or black, so that:
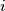
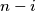
(i) and always receive the same color, and
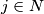
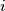
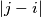
(ii) for some , relatively prime to , and receive the same color for all
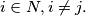
Prove that all numbers in must receive the same color.
%V0
Each of the numbers in the set $N = \{1, 2, 3, \cdots, n - 1\}$, where $n \geq 3$, is colored with one of two colors, say red or black, so that:
(i) $i$ and $n - i$ always receive the same color, and
(ii) for some $j \in N$, relatively prime to $n$, $i$ and $|j - i|$ receive the same color for all $i \in N, i \neq j.$
Prove that all numbers in $N$ must receive the same color.
Izvor: Međunarodna matematička olimpijada, shortlist 1985
Školjka 
, where 
, is colored with one of two colors, say red or black, so that:
and 
always receive the same color, and
, relatively prime to 
, 
receive the same color for all 
must receive the same color.