IMO Shortlist 1999 problem G6
Dodao/la:
arhiva2. travnja 2012. Two circles
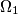
and
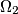
touch internally the circle
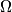
in M and N and the center of
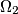
is on
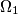
. The common chord of the circles
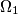
and
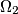
intersects
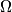
in
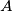
and
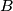
.
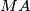
and
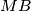
intersects
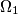
in
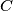
and
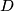
. Prove that
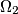
is tangent to
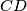
.
%V0
Two circles $\Omega_{1}$ and $\Omega_{2}$ touch internally the circle $\Omega$ in M and N and the center of $\Omega_{2}$ is on $\Omega_{1}$. The common chord of the circles $\Omega_{1}$ and $\Omega_{2}$ intersects $\Omega$ in $A$ and $B$. $MA$ and $MB$ intersects $\Omega_{1}$ in $C$ and $D$. Prove that $\Omega_{2}$ is tangent to $CD$.
Izvor: Međunarodna matematička olimpijada, shortlist 1999