IMO Shortlist 2004 problem A1
Dodao/la:
arhiva2. travnja 2012. Let
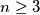
be an integer. Let
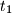
,
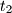
, ...,
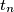
be positive real numbers such that
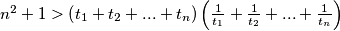
.
Show that
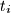
,
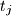
,
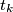
are side lengths of a triangle for all
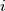
,
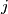
,
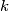
with
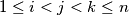
.
%V0
Let $n \geq 3$ be an integer. Let $t_1$, $t_2$, ..., $t_n$ be positive real numbers such that
$n^2 + 1 > \left( t_1 + t_2 + ... + t_n \right) \left( \frac{1}{t_1} + \frac{1}{t_2} + ... + \frac{1}{t_n} \right)$.
Show that $t_i$, $t_j$, $t_k$ are side lengths of a triangle for all $i$, $j$, $k$ with $1 \leq i < j < k \leq n$.
Izvor: Međunarodna matematička olimpijada, shortlist 2004