IMO Shortlist 2009 problem G1
Dodao/la:
arhiva2. travnja 2012. Let
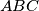
be a triangle with
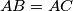
. The angle bisectors of
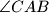
and
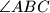
meet the sides
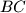
and
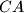
at
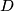
and
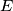
, respectively. Let
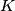
be the incentre of triangle
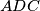
. Suppose that
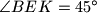
. Find all possible values of
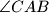
.
Jan Vonk, Belgium, Peter Vandendriessche, Belgium and Hojoo Lee, Korea
%V0
Let $ABC$ be a triangle with $AB = AC$ . The angle bisectors of $\angle C AB$ and $\angle AB C$ meet the sides $B C$ and $C A$ at $D$ and $E$ , respectively. Let $K$ be the incentre of triangle $ADC$. Suppose that $\angle B E K = 45^\circ$ . Find all possible values of $\angle C AB$ .
Jan Vonk, Belgium, Peter Vandendriessche, Belgium and Hojoo Lee, Korea
Izvor: Međunarodna matematička olimpijada, shortlist 2009