IMO Shortlist 2012 problem G5
Kvaliteta:
Avg: 3,0Težina:
Avg: 8,0 Let  be a triangle with
be a triangle with 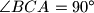 , and let
, and let 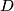 be the foot of the altitude from
be the foot of the altitude from 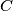 . Let
. Let 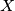 be a point in the interior of the segment
be a point in the interior of the segment 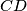 . Let
. Let 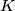 be the point on the segment
be the point on the segment  such that
such that 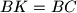 . Similarly, let
. Similarly, let 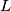 be the point on the segment
be the point on the segment 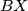 such that
such that 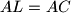 . Let
. Let  be the point of intersection of
be the point of intersection of  and
and 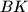 .
.
Show that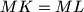 .
.
Proposed by Josef Tkadlec, Czech Republic
 be a triangle with
be a triangle with 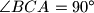 , and let
, and let 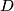 be the foot of the altitude from
be the foot of the altitude from 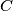 . Let
. Let 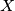 be a point in the interior of the segment
be a point in the interior of the segment 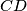 . Let
. Let 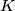 be the point on the segment
be the point on the segment  such that
such that 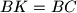 . Similarly, let
. Similarly, let 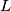 be the point on the segment
be the point on the segment 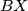 such that
such that 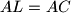 . Let
. Let  be the point of intersection of
be the point of intersection of  and
and 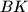 .
.Show that
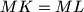 .
.Proposed by Josef Tkadlec, Czech Republic
Izvor: Međunarodna matematička olimpijada, shortlist 2012
 Školjka
Školjka 
